5. Výberové charakteristiky

Obsah

Geometrický priemer

Geometrický priemer  je vhodný vtedy, keď má zmysel počítať súčin pozorovaných hodnôt. Vypočíta sa ako n-tá odmocnina zo súčinu n pozorovaní:

(5.4a)

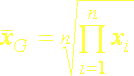
(5.4b)

Dá sa použiť aj pre údaje roztriedené do k tried vo forme váženého geometrického priemeru

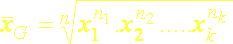
(5.4c)

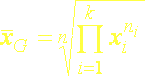
(5.4d)

pričom pre súčet váh n_i platí rovnaký vzťah (5.3) ako pre vážený aritmetický priemer.
Geometrický priemer sa obvykle používa pre veličiny, merané na logaritmickej stupnici. Ak zlogaritmujeme (pri základe z) obidve strany vzorca (5.4a), dostaneme:

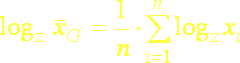
(5.5a)

a pre vážený geometrický priemer:

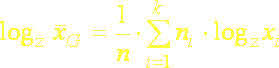
(5.5b)

Znamená to, že logaritmus geometrického priemeru je rovný (aritmetickému) priemeru zlogaritmovaných pozorovaní. Tento vzťah je veľmi užitočný pre jednoduchší výpočet geometrického priemeru, pretože n-tú odmocninu nahrádza logaritmom (najmä ak nemáme práve poruke vhodný počítačový program). Pre výpočet geometrického priemeru (jednoduchého alebo váženého) potom platí:

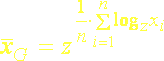
(5.6a)

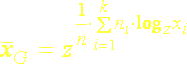
(5.6b)

Za základ logaritmu sa obvykle berie z = 10 (desiatkový logaritmus) alebo z = e (prirodzený logaritmus), ale vzťahy sú platné všeobecne pre ľubovoľný základ z.
Geometrický priemer nepoužívame pre pozorovania, ktoré nadobúdajú nulové alebo záporné hodnoty. Je veľmi vhodný napríklad v situáciách, keď meriame hodnoty v postupne riedených roztokoch alebo keď je rozdelenie hodnôt asymetrické a logaritmická transformácia ho transformuje do symetrického tvaru.