2. Meranie a spracovanie výsledkov merania

Obsah

2.1. Chyby merania

    Fyzikálne veličiny, ktoré sú výsledkom merania, sa odlišujú od matematických veličín tým, že ich môžeme odmerať len s určitou presnosťou. Namiesto presnej hodnoty, t.j. bodu v súradnicovej sústave, dokážeme určiť iba interval, v ktorom sa nachádza hľadaná hodnota meranej veličiny. Táto nepresnosť - neurčitosť merania môže mať svoje príčiny v meranom objekte alebo v meracej aparatúre.

    Pri bežných meraniach s komerčnými meracími prístrojmi, od ktorých požadujeme len primeranú presnosť, sa uspokojíme s nameranou hodnotou bez ďalšieho skúmania, či je výsledok správny alebo chybný a do akej miery. K tomu prispieva určitá dôvera vo funkčnosť prístroja a jeho životnosť. Pri rutinnom sledovaní ide často o sotva zvládnuteľnú námahu a výdavky, ktoré by boli spojené so stále opakovaným stanovovaním a dokazovaním presnosti merania. Typickým príkladom je bežné meranie telesnej teploty lekárskym teplomerom.

    Napriek tomu platí: Údaj konečného výsledku meracej úlohy je úplný až vtedy, keď je pri číselnej hodnote a jednotke miery uvedená aj chyba merania.

    Odhad chyby merania je rovnako dôležitý ako samotné meranie. Obzvlášť nezanedbateľná je diskusia ohľadom chýb pri sledovaniach pomocou meracích aparatúr neznámej akosti alebo pri experimentoch, ktoré si vyžadujú vysokú presnosť. Príkladom takýchto „experimentov“ je napríklad stanovenie obsahu rozličných látok v krvi, ktoré majú diagnostický význam.

    Označme Δx chybu meranej veličiny x₀ (obr. 2.1). Za predpokladu, že Δx ≥ 0 (a v celom nasledujúcom texte predpokladáme, že chyba je nezáporná bez ohľadu na spôsob jej výpočtu, pokiaľ výslovne nie je uvedené inak), úplný údaj výsledku úlohy je

           (x₀ ± Δx) jednotiek

(2.1)

      
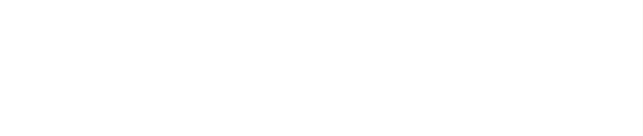
Obr. 2.1: Grafické znázornenie údaja meranej veličiny x₀
s absolútnou chybou ± Δx.

    Uvedenie fyzikálnej jednotky je nevyhnutné, inak je výsledok nesprávny. Vo fyzike a vo všetkých vedách, ktoré pracujú s fyzikálnymi veličinami vrátane medicíny, totiž číslo bez fyzikálnej jednotky nemá žiaden význam.
    Niekedy sa môžeme stretnúť aj s iným spôsobom zápisu. Chybu býva zvykom udávať v percentách nameranej hodnoty ako percentuálnu chybu

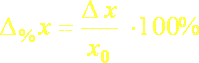
(2.2)

    Chybu merania s označením Δx nazývame absolútna chyba merania a má rovnaký fyzikálny rozmer ako meraná fyzikálna veličina, t.j. udáva sa v rovnakých fyzikálnych jednotkách. Chyba merania s označením Δ_%x sa nazýva percentuálna chyba merania a podobne ako všetky údaje v percentách je bezrozmerná.
    Chyba merania s označením Δ_rx, vyjadrená vzťahom

(2.3)

sa nazýva relatívna chyba merania a je bezrozmerná.