5. Výberové charakteristiky

Obsah

Priemery

    Jednou z možností sú rôzne priemery, ktoré predstavujú určité charakteristiky súboru, akýsi „stredný“ – reprezentatívny údaj.
Priemer (aritmetický priemer)  používame vtedy, keď čísla môžeme skutočne sčítavať, t.j. ide o kvantitatívne znaky merané na číselnej stupnici. Vypočítame ho tak, že sčítame všetky hodnoty jednotlivých meraní x₁ , x₂ , x₃ ,...,x_n a súčet delíme počtom meraní (rozsahom súboru) n:

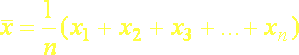
(5.1a)

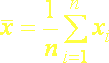
(5.1b)

Výpočet priemeru má význam iba vtedy, keď všetky merania boli urobené za rovnakých podmienok. Preto sa treba vopred presvedčiť, že všetky premenné veličiny, ktoré ovplyvňujú meranie, sa dajú udržať čo najviac konštantné.
Ten istý priemer dostaneme kombináciou rôznych meraných hodnôt.

Nevýhodou priemeru je jeho veľká citlivosť na okrajové hodnoty. Napriek tomu stanovenie priemeru vedie k presnejšej výpovedi o fyzikálnom meraní ako jediná hodnota, pretože rozptyl meraných hodnôt sa čiastočne kompenzuje, pokiaľ ide o náhodné chyby. Systematické chyby sa pritom nezmenšia, pretože každé meranie je skreslené rovnakým smerom. Priemer merania  treba odlišovať od skutočnej strednej hodnoty μ. Obidve hodnoty sú identické len vtedy, keď sa počet meraní  n blíži k nekonečnu. Hodnota μ znamená hodnotu merania bez náhodných chýb. Ak však jednotlivé hodnoty obsahujú systematickú chybu, ani pri veľkom počte meraní nedokážeme určiť skutočnú hodnotu (pozri kap. 2.3.).