2. Meranie a spracovanie výsledkov merania

Obsah

       d.) Relatívna chyba závislej veličiny ƒ, ktorá je funkciou súčinu alebo podielu dvoch nezávislých veličín x₁ a x₂, sa rovná druhej odmocnine súčtu druhých mocnín relatívnych chýb oboch veličín Δ_rx₁ a Δ_rx₂

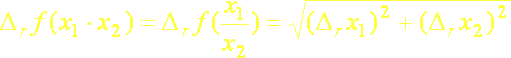
(2.8)

      e.) Relatívna chyba závislej veličiny ƒ, ktorá je funkciou k-tej mocniny nezávislej veličiny x, sa rovná súčinu konštanty k  a relatívnej chyby nezávislej veličiny Δ_rx:

      Δ_r ƒ(x^k) = k . Δ_r x

(2.9)

      f.) Relatívna chyba závislej veličiny ƒ, ktorá je funkciou k-tej odmocniny nezávislej veličiny x, sa rovná podielu relatívnej chyby nezávislej veličiny Δ_rx a konštanty k:

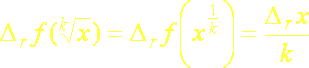
(2.10)

      g.) Absolútna chyba závislej veličiny ƒ, ktorá je funkciou prirodzeného logaritmu nezávislej veličiny x, sa číselne rovná relatívnej chybe nezávislej veličiny Δ_rx:

      Δƒ(ln x) = Δ_rx

(2.11)