5. Výberové charakteristiky
Obsah
Modus
Modus 
je hodnota, ktorá sa v súbore dát vyskytuje najčastejšie. Používa sa najmä pre kvalitatívne, spravidla nominálne znaky, hoci môže byť vhodnou charakteristikou aj pre kvantitatívne znaky.
V súboroch A a B z príkladu 5.2 sa iba jedna hodnota vyskytovala viackrát ako iné hodnoty. Graf rozdelenia početnosti takýchto súborov (histogram, frekvenčný polygón) by mal iba jeden vrchol (unimodálne rozdelenie početnosti). Pri reálnych meraniach sa môžeme stretnúť s grafmi, ktoré budú mať viac separovaných vrcholov (2 alebo 3). Poloha 2. (3.) vrcholu zodpovedá polohe 2. (3.) modusu (bimodálne (trimodálne) rozdelenie početnosti). Frekvencia výskytu hodnôt veličiny pre jednotlivé modusy môže, ale nemusí byť rovnaká.
Ak však pri meraní získame graf viacvrcholového rozdelenia, v prvom rade treba meranie analyzovať a dôsledne posúdiť, či naozaj všetky hodnoty patria do jedného súboru. Mohlo sa totiž stať, že pri meraní sme nezohľadnili nejaký parameter, ktorý v skutočnosti hrá dôležitú úlohu v tom zmysle, že neumožňuje spojiť všetky získané hodnoty do jediného súboru. V ďalšom texte budeme preto uvažovať iba unimodálne rozdelenia.
Pre kvantitatívne znaky, ktoré sú roztriedené do intervalov, určíme modálny interval (má najvyššiu početnosť) a modus stanovíme interpoláciou vzhľadom na početnosti susedných intervalov podľa niektorého z nasledovných vzťahov:
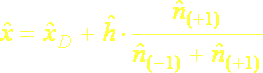
(5.9)
alebo
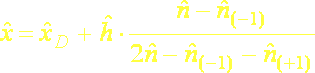
(5.10)
kde 
je dolná hranica modálneho intervalu, 
je jeho dĺžka,
je početnosť predchádzajúceho intervalu, 
je početnosť modálneho intervalu a 
je početnosť nasledujúceho intervalu. Pri odvodení týchto vzťahov sa vychádzalo z predpokladu, že modus sa viac „prikloní“ k početnejšiemu intervalu. Ďalší vzťah na výpočet modusu vychádza z kvadratickej aproximácie, t.j. predpokladá sa, že modus je vrcholom paraboly:
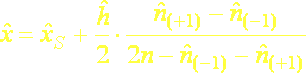
(5.11)
kde 
je stred modálneho intervalu. Modus nie je ovplyvňovaný hodnotami všetkých prvkov výberu. Využíva sa najmä na vystihnutie najtypickejšej hodnoty znaku.
Ak je rozdelenie v štatistickom súbore úplne symetrické vzhľadom na určitú hodnotu znaku xi = a, ktorá sa vyskytuje v súbore najčastejšie, teda ak početnosti hodnôt od nej nižších aj vyšších klesajú rovnako na obidve strany (obr. 5.1 v strede), platí:
(5.12)
Ak rozdelenie nie je symetrické, aritmetický priemer je vzhľadom na modus posunutý smerom k pretiahnutej, voľnejšie klesajúcej časti krivky rozdelenia početnosti a medián je približne v tretine vzdialenosti od aritmetického priemeru smerom k modusu. Pre ľavostranné asymetrické rozdelenie (maximum krivky rozdelenia početnosti – modus – je vľavo) platí (obr. 5.1 vľavo):
(5.13)
Pre pravostranné asymetrické rozdelenie (maximum krivky rozdelenia početnosti – modus – je vpravo) platí (obr. 5.1 vpravo):
(5.14)
Vo všeobecnosti medzi aritmetickým priemerom, mediánom a modusom približne platí vzťah, ktorý možno využiť na približné určenie modusu v štatistickom súbore:
(5.15)
ktoré vyjadruje, že rozdiel medzi priemerom a modusom je trojnásobkom rozdielu medzi priemerom a mediánom.
Obr. 5.1: Ukážka spojitého symetrického rozdelenia (hore) a spojitých asymetrických rozdelení (ľavostranné vľavo dolu a pravostranné vpravo dolu).
