5. Výberové charakteristiky

Obsah

Stredná chyba aritmetického priemeru

   Často nás nezaujíma rozptyl jednotlivých hodnôt okolo ich priemeru, ale spoľahlivosť, s akou sme určili priemer merania ako jeho najlepšiu hodnotu, teda chyba priemeru vzhľadom k skutočnej strednej hodnote μ. Pretože aj priemer je zaťažený náhodnou chybou, odchyľuje sa od skutočnej hodnoty. Je zrejmé, že priemer = 5,0 získaný z 3 široko rozptýlených jednotlivých meraní nie je veľmi spoľahlivý a môže sa odlišovať od skutočnej hodnoty.
Čím väčší je ale počet meraní, tým presnejšie určíme strednú hodnotu. Toto vyplýva aj zo vzorca na výpočet strednej chyby priemeru se_x , ktorý sa od vzorca na výpočet smerodajnej odchýlky s_x líši tým, že ešte sa delí druhou odmocninou počtu meraní

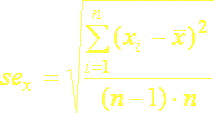
(5.25a)

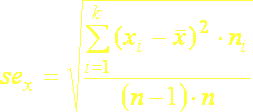
(5.25b)

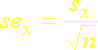
(5.25c)

   Skutočná hodnota μ meranej veličiny leží s veľkou pravdepodobnosťou v intervale ± se_x (obr. 5.2). Stredná chyba priemeru sa využíva napríklad pri výpočte intervalov spoľahlivosti a pri konštrukcii štatistických testov. Udáva sa v rovnakých jednotkách ako nameraná veličina.

Obr. 5.2: Skutočná hodnota μ meranej veličiny leží s veľkou
pravdepodobnosťou v intervale vyznačenom
obojstrannou šípkou. Krivka predstavuje absolútnu
alebo relatívnu početnosť spojitej veličiny.

   Zo strednej chyby priemeru vyplýva otázka: Aký veľký má byť meraný súbor (t.j. aké veľké má byť n) alebo kedy sa námaha ďalších meraní zúročí vo výraznom zmenšení chyby? Zo vzťahov (5.22) vidíme, že ak k 3 existujúcim meraniam pridáme ďalšie 3, zmenšíme rozptyl meraní asi na 40 % pôvodnej hodnoty. Ak sme už však 20 meraní urobili, na rovnaké percentuálne zmenšenie rozptylu treba urobiť ďalších 28 meraní. Pri už urobených 30 (40) meraniach treba na rovnaké percentuálne zmenšenie rozptylu urobiť ešte ďalších 43 (58) meraní. Pri n < 20 sa teda vo všeobecnosti oplatí zvyšovať počet meraní, pri n > 20 má význam robiť ďalšie merania iba vo výnimočných prípadoch. 
Stredná chyba priemeru sa používa tiež na približné určenie presnosti odhadu. Odhad považujeme za veľmi dobrý vtedy, ak stredná chyba je menej ako 5 % veľkosti priemeru, t.j. napríklad:

(5.26)

   Odhad považujeme za dobrý vtedy, ak stredná chyba je menej ako 10 % veľkosti priemeru. Za dostatočný považujeme odhad vtedy, ak stredná chyba je medzi 10 % až 15 % hodnoty priemeru. Slabý (nedostatočný) odhad je so strednou chybou väčšou ako 15 %.